Инвертированный маятник
Пример: Инвертированный маятник
The problem is to balance a pole on a mobile platform that can move in only two directions, to the left or to the right.
Задача должна балансировать полюс на подвижной платформе, которая может перемещать в только в двух направлениях, налево или направо
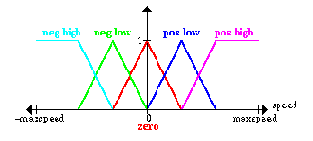
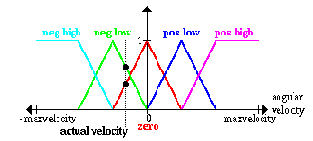
First of all, we have to define (subjectively) what high speed, low speed etc. of the platform is; this is done by specifying the membership functions for the fuzzy_sets
Прежде всего мы должны определить (субъективно) что такое высокая скорость, низкая скорость и т.д. платформы; это выполнено, при помощи определения функции принадлежности для нечеткого_множества
· negative high (cyan)
· negative low (green)
· zero (red)
· positive low (blue)
· positive high (magenta)
· отрицательно высокая скорость (голубым)
· отрицательно низкая (зеленым)
· Нулевая (красным)
· Положительно низкая (синим)
· Положительно высокая (сиреневым)
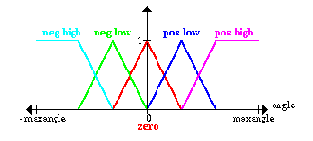
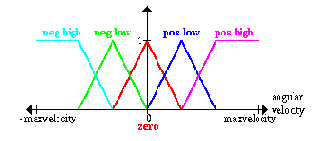
The same is done for the angle between the platform and the pendulum and the angular velocity of this angle:
Тот же самый выполнен для угла между платформой и маятником и угловым ускорением этого угла:
Please notice that, to make it easier, we assume that in the beginning the pole is in a nearly upright position so that an angle greater than, say, 45 degrees in any direction can - by definition - never occur.
Пожалуйста заметьте, что, чтобы делать это проще, мы принимаем, что в начале полюс находится в почти вертикальном положении так, чтобы угол большее чем, скажем, 45 градусов в любом направлении мог - по определению - никогда не мог быть.
On the next page we will set up some rules that we wish to apply in certain situations.
Далее мы установим некоторые правила, которые мы желаем применить в некоторых ситуациях.
Now we give several rules that say what to do in certain situations:
Теперь мы даем несколько правил, которые говорят, что делать в некоторых ситуациях:
Consider for example that the pole is in the upright position (angle is zero) and it does not move (angular velocity is zero). Obviously this is the desired situation, and therefore we don't have to do anything (speed is zero).
Предположим например, что полюс находится в вертикальном положении (угол - нуль) и он не двигается (угловое ускорение - нуль). Очевидно это - желательная ситуация, и следовательно мы не должны делать что - нибудь (скорость - нуль).
Let's consider another case: the pole is in upright position as before but is in motion at low velocity in positive direction. Naturally we would have to compensate the pole's movement by moving the platform in the same direction at low speed.
Давайте рассматривать другой случай: полюс находится в вертикальном положении как прежде, но находится в движении с низким ускорением в положительном направлении. Естественно мы были бы должны компенсировать перемещение полюса, перемещая платформу в том же самом направлении с низкой скоростью.
So far we've made up two rules that can be put into a more formalized form like this:
Пока мы составили два правила, которые могут быть помещены в более формализованную форму подобно этому:
· If angle is zero and angular velocity is zero then speed shall be zero.
· If angle is zero and angular velocity is pos. low then speed shall be pos. low.
· Если угол - нуль, и угловая скорость - нуль, тогда скорость, будет нуль.
· Если угол - нуль, и угловое ускорение - pos. Тогда низкая скорость должна быть pos.
Низко.
We can summarize all applicable rules in a table:
Мы можем суммировать все соответствующие правила в таблице:
| угол
|
скорость | NH NL Z PL PH
----------+------------------------------
у NH | NH
с NL | NL Z
к Z | NH NL Z PL PH
о PL | Z PL
р PH | PH
where NH is a (usual) abbreviation for negative high, NL for negative low etc.
Где NH - (обычное) сокращение для отрицательно высокой, NL для отрицательно низкой и т.д.
On the next pages we will show how these rules can be applied with concrete values for angle and angular velocity.
На следующих страницах мы покажем, как эти правила могут применяться с конкретными значениями для угла и углового ускорения.
We are going to define two explicit values for angle and angular velocity to calculate with. Consider the following situation:
Мы собираемся определить два явных значения для угла и углового ускорения, чтобы вычислять правила. Рассмотрим следующую ситуацию:
An actual value for angle:
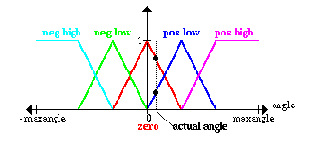
Фактическое значение для угла:
An actual value for angular velocity:
Фактическое значение для угловой скорости:
On the next page you will be able to watch how we apply our rules to this actual situation.
Далее Вы будете наблюдать, как мы применяем наши правила к этой фактической ситуации.
Let's apply the rule
Давайте применим правило
If angle is zero and angular velocity is zero then speed is zero
Если угол - нуль, и угловое ускорение - нуль, тогда скорость - нуль
to the values that we've selected on the previous page:
К значениям, которые мы выбрали на ранее:
Click on the symbol to see how the result develops:
Вот как результат разрабатывается:
1. Угол
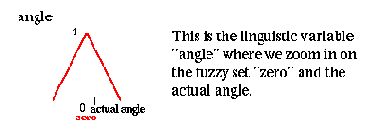
ноль; фактический угол.
Это - лингвистическая переменная "угол", здесь мы увеличиваем на нечетком множестве "нуль" и фактический угол.
2. Угол и угловое ускорение
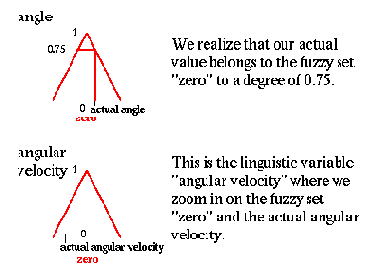
ноль; фактический угол.
Ноль; фактическое угловое ускорение
Мы реализуем, что наше фактическое значение принадлежит нечеткому множеству "нуль" со степенью 0.75
Это - лингвистическая переменная "уголовое ускорение", здесь мы увеличиваем на нечетком множестве "нуль" и фактическое уголовое ускорение.
3. Угол и угловое скорение
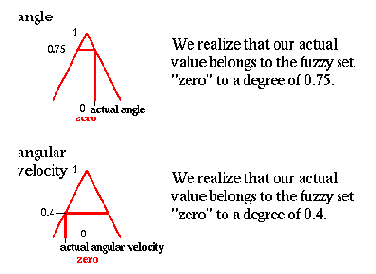
Мы реализуем, что наше фактическое значение принадлежит нечеткому множеству "нуль" со степенью 0.75
Мы реализуем, что наше фактическое значение принадлежит нечеткому множеству "нуль" со степенью 0.4
4. Угол и угловое ускорение
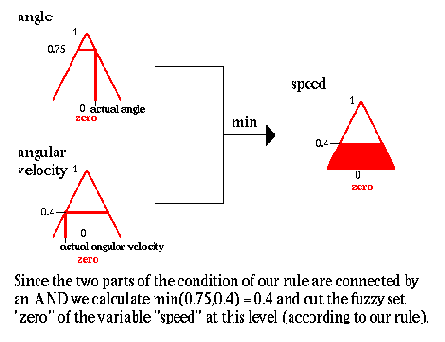
Так как две части условия нашего правила соединены, И мы вычисляем минимум (0.75,0.4) = 0.4 и обрезаем нечеткое множество "нуль" переменной "скорость" на этом уровне (согласно нашему правилу).
Only four rules yield a result (they fire), and we overlap them into one single result.
Только четыре правила производят результат (они огонь), и мы перекрываем их в один единственный результат.
As shown on the previous page the result yielded by the rule
if angle is zero and angular velocity is zero then speed is zero
is:
Как показано выше результат, выданный правилом
Если угол - нуль, и угловое ускорение - нуль, тогда скорость - нуль:
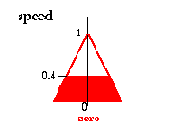
The result yielded by the rule
if angle is zero and angular velocity is negative low then speed is negative low
is:
Результат, выданный правилом
Если угол - нуль, и угловое ускорение отрицательно низко, тогда скорость, отрицательна низка:
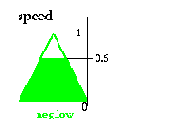
The result yielded by the rule
if angle is positive low and angular velocity is zero then speed is positive low
is:
Результат, выданный правилом
Если угол положителено низок, и угловое ускорение - нуль, тогда скорость, положительна низока:
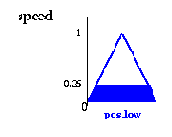
The result yielded by the rule
if angle is positive low and angular velocity is negative low then speed is zero
is:
Результат, выданный правилом
Если угол положительно низок, и угловое ускорение отрицательно низко, тогда скорость - нуль:
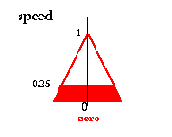
These four results overlapped yield the overall result:
Эти четыре результата, дают полный результат:
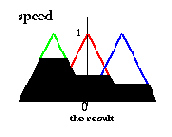
The result of the fuzzy controller so far is a fuzzy set (of speed), so we have to choose one representative value as the final output. There are several heuristic methods (defuzzification methods), one of them is e.g. to take the center of gravity of the fuzzy set:
Результат нечеткого контроллера пока - нечеткое множество (скорости), так что мы должны выбрать одно представляющее значение как окончательный результат. Имеются отдельные эвристические методы (defuzzification(не нечеткие) методы), по одному из которых должен например брать центр тяжести нечеткого множества:
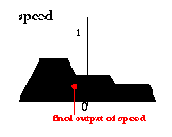
The whole procedure is called Mamdani controller.
Целая процедура называется Mamdani контроллером.
The next page deals with applications of Fuzzy Logic.
Далее имеем дело с приложениями Нечеткой Логики.
Приложения Нечеткой Логики
First, we shall look at the fitness of Fuzzy Control in general terms.
Сначала, мы рассмотрим пригодность Нечеткого Управления общим условиям.
The employment of Fuzzy Control is commendable...
· for very complex processes, when there is no simple mathematical model
· for highly nonlinear processes
· if the processing of (linguistically formulated) expert knowledge is to be performed
Использование Нечеткого Управления - похвально ...
· Для очень комплексных процессов, когда нет простой математической модели
· Для очень нелинейных процессов
· Если обработки (лингвистически сформулированно) экспертного знания должна выполниться
The employment of Fuzzy Control is no good idea if...
· conventional control theory yields a satisfying result
· an easily solvable and adequate mathematical model already exists
· the problem is not solvable
Использование Нечеткого Управления не имеет смысла если ...
· Стандартная теория управления производит удовлетворяющий результат
· Легко разрешимая и адекватная математическая модель уже существует
· Задача не разрешима
